이 대회의 목적은 주어진 데이터를 잘 설명할 수 있는 모델을 만들어 추후 불량품과 정상품을 선발해내는 것입니다.

이를 위해서 가장 중요한 것은 모델 선정과 개발이지만, 모델의 성능을 높이는 것은 쉬운 일이 아닙니다.

그렇기에 모델의 성능을 높이기 위해서는 해당 모델에 대한 깊이 이해가 중요하다는 것을 공유하고자 이 글을 작성하게 되었습니다.

이 글에서 다룰 모델은 Baseline 모델인 Mulit-output Linear Regression입니다. 해당 모델의 수식을 보시면:

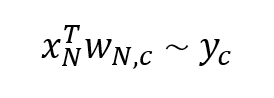여기서 x와 y, w는 각각 다음과 같습니다:

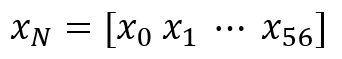
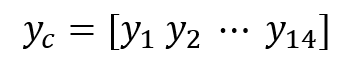
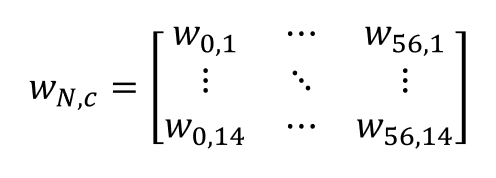
이 모델은 사실 c값에 1~14를 넣어가며 다중회귀분석을 반복할 뿐인 모델입니다.

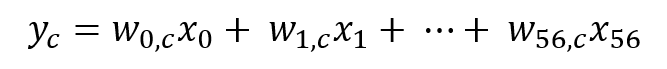
그렇기에 중요한 것은 회귀분석에 대한 이해입니다. 회귀분석(OLS)은 6가지 가정을 전제로 할 때 최적의 성능을 발휘할 수 있습니다.

그 상태를 BLUE(Best Linear Unbiased Estimator)라고 하고, 본 대회에서 현실적으로 살펴볼 수 있는 가정은 다음과 같습니다.

1. Zero mean: 잔차들의 평균이 0이 되어야 함을 의미합니다.

이는 검증용 데이터셋(ex: validation_y)과 모델로 추정한 값(ex: prediction_y)를 뺀 값의 평균으로 구할 수 있습니다.

실제로 구해보면 0과 큰 차이가 나지 않는 것을 확인할 수 있습니다.

2. Homoskedasticity: 잔차들이 등분산성을 지니고 있어야 함을 의미합니다.

이를 검증하기 위해서 Goldfeld-Quandt를 사용했습니다.

해당 검정의 귀무가설은 '데이터가 등분산성을 지닌다'로 p값이 0.05이상 나오면 귀무가설을 기각할 수 없는 형태입니다.

검정 결과 Y_01에 대한 잔차를 제외하고는 모두 등분산성을 지니고 있다고 할 수 있습니다.

이 경우 X값들보단 Y_01값 때문에 생긴 문제인데,  Y_01값을 직접 건드리면 해당 대회 평가 점수에 문제가 생기기에 넘어가겠습니다.

3. No-autocorrelation: 잔차들에게 자기상관성이 없어야 함을 의미합니다.

이를 검증하기 위해서 Durbin-Watson test를 이용했습니다. 이 검정은 0~4 사이의 값을 가지고, 2에 가까울수록 자기상관성이 없음을 뜻합니다.

검정결과 전부 2에 가까운 것을 확인할 수 있습니다.

4. Normality: 잔차들이 정규분포를 따라야 함을 의미합니다.

이 가정을 만족하기 위해서 모든 잔차들에게 정규성 검정을 시행할 필요는 없습니다.

실제로 이를 만족시키는 경우가 매우 적을 뿐더러, 보통 이 가정을 만족하기 위해서는 대수의 법칙을 사용합니다.

결국 데이터의 수가 중요하고, 본 대회에서는 몇만개의 데이터를 사용하고 있기도 하고, 데이터를 더 추가할 방법도 없기에 넘어가겠습니다.

결론적으로 본 대회에서 주어진 독립변수들은 해당 가정들을 크게 위배하지 않습니다.

하지만 다중회귀분석을 할 때에만 위 가정들을 제외하고도 또 고려해야 할 요소가 있습니다. 바로 다중공선성(Muliticollinearity) 문제입니다.

이는 독립변수(X값)들 간에 강한 상관관계가 나타날 때 생기는 문제입니다.

다중회귀분석에서 회귀계수(coefficient)는 해당 변수가 얼마나 강한 영향력을 가지고 있는지 나타내는 지표입니다.

그런데 어떤 변수 A가 다른 변수 B와 강한 상관관계를 가지고 있다면, 해당 변수 A가 가져야 하는 영향력을 B와 나눠 가지게 됩니다.

만약 어떤 종속변수를 추정하는데 A가 B보다 더 중요하다고 할 때, B로 인해서 상대적으로 A의 영향력이 감소하면, 해당 회귀분석 모델의 에러가 커지게 됩니다.

물론 반대의 경우도 성립하고, 상대적으로 에러에 별 영향을 미치지 않을 수도 있습니다.

확실한 것은 다중공선성이 존재할 경우 에러의 변동이 심해지고, 추정의 정확도가 떨어진다는 것입니다.

먼저 다중공선성 문제를 확인하기 위해 상관계수를 확인할 수 있습니다.

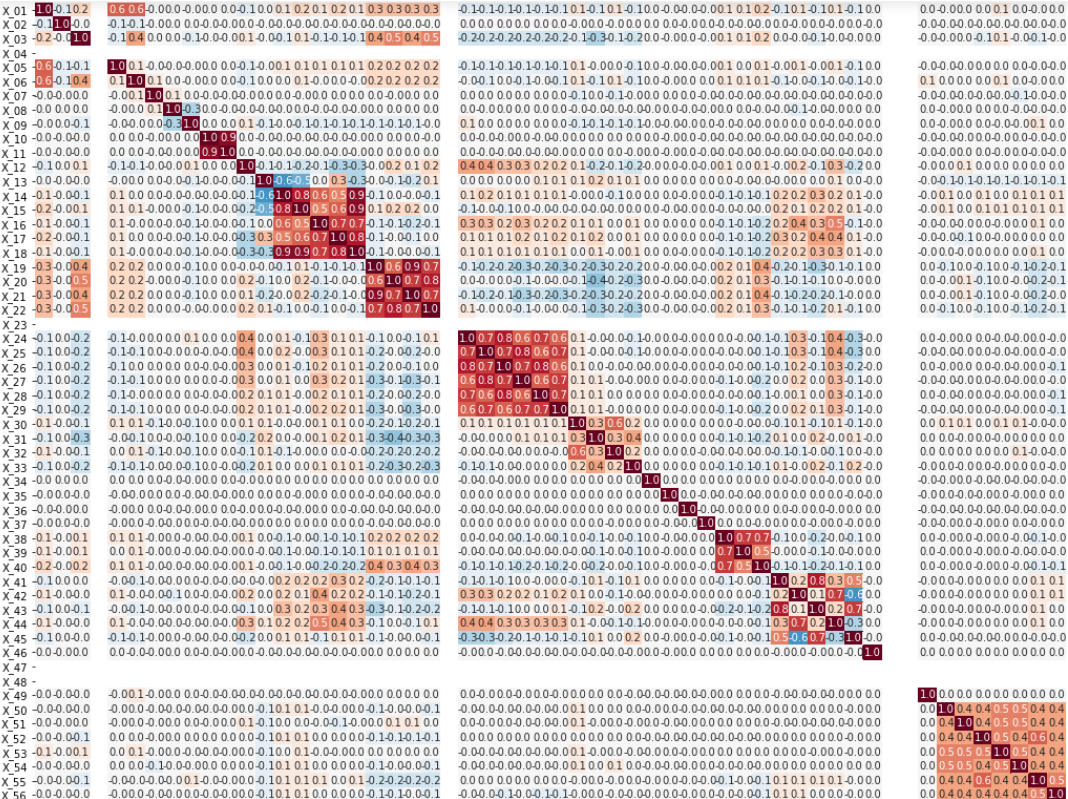
대회에 참가하셔서 상관분석 해보신 분들은 다 아시겠지만,

연속되는 특정 변수들의 집합에서 상관관계가 높게 나타납니다.

사실 이는 어쩔 수 없는 것이, 변수들 자체가 그렇게 구성되어 있습니다.

대회 토크에 문의사항에 대한 답변에 나와있듯,

X_19 ~ X_22 같은 경우 같은 대상을 다른 장비로 측정한 값입니다.

대상이 같기에 상관성이 높은 것은 어쩔 수 없는 것입니다.

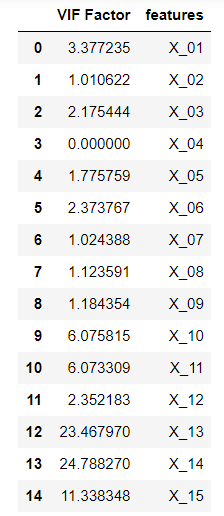또한 다중공선성 문제를 엄밀히 진단하기 위해 사용하는 것이 VIF(Variance Influence Factor: 분산 팽창 인수)입니다.

VIF는 특정 독립변수가 다른 독립변수에 의해 설명되는 정도를 나타내는 값이며, 이 값이 큰 변수일수록 다중공선성

문제를 발생시킬 수 있습니다. 보통은 10이상의 값을 가질 때 다중공선성 문제가 있다고 판단하는데,

대회에서 제공하는 데이터셋의 경우 다중공선성 문제가 꽤 심각합니다.

이를 해결하기 위해서는 다중공선성 문제를 발생시킬 수 있는 변수의 영향력을 감소시켜야 합니다.

보통은 그 변수를 삭제하는 식으로 해결하지만, 본 대회처럼 많은 양의 독립변수를 이용해서 다중회귀분석을 하는 경우,

특정 변수의 삭제는 오히려 모델의 성능 저하를 야기할 수 있습니다.

(제 경우 실제로 하락했습니다)

이 경우 사람이 일일히 feature engineering을 통해 변수 변형과 삭제를 하기보다는,

문제를 발생시킬 수 있는 변수의 처리를 컴퓨터의 손에 맡기는 것이 좋습니다. 그 방법이 바로 규제 회귀입니다.

규제 회귀에는 대표적으로 라쏘(Lasso)와 릿지(Ridge)가 있습니다. 전부 모델에 규제항을 추가하여 특정 변수에 너무 의존하는 경향을 줄이는 방법들입니다.

차이가 있다면 라쏘는 특정 변수들의 계수를 0으로 만들 수 있고, 릿지는 계수를 0으로 만들 수 없다는 겁니다.

앞서 말했듯 특정 변수의 삭제(0으로 만들기)는 오히려 모델 성능의 저하를 불러올 수 있습니다.

그렇기에 다중공선성 문제를 해결하되, 변수를 삭제하지 않기 위해 라쏘회귀로 Multi-output Regression을 진행하겠습니다.

그리고 그 결과 Baseline모델보다 성능이 향상되었습니다. (대회평가 NRMSE기준 0.2292... -> 0.2291...)

이제 이 회귀모델의 성능을 향상시키기 위해서는 하이퍼 파라미터 튜닝을 통해 최적 alpha값을 구해야 하지만,

그건 이 글의 목적이 아니기 때문에 넘어가겠습니다.

이 글에서 시사하고 싶은 것은 같은 유형의 모델을 사용하더라도, 그 모델을 어떤 원리로 작동하는지 이해하고 있으면

그에 맞춰서 성능을 향상시킬 방법을 찾을 있다는 것을 공유하기 위해서였습니다.

해당 과정에 대한 코드는 코드 공유에 업로드 하겠습니다.

긴 글 읽어주셔서 감사합니다.